Combination: In combinatorial mathematics, a combination is an un-ordered collection of distinct elements, usually of a prescribed size and taken from a given set.

Permutation:In combinatorics, a permutation is usually understood to be a sequence containing each element from a finite set once, and only once

(Wikipedia definitions)
It is very crucial to understand these terms.
For me, everything in this unit went swimmingly well until we learned about this:

oh boy... But I realized after we did some questions, and with further exploring this, everything went a whole lot better...

That is pascals triangle. Don't forget some nifty tricks in the triangle, like 2^x rule and how it corresponds with the row number, and the 11^x, and also the good old hockey stick pattern.
To view all possible poker hand probabilities, go to this link!
I didn't find much trouble with the poker hands because I'm a big fan of the game.
Well this sums up my bob post, the next bob is bob by the way!


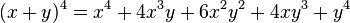
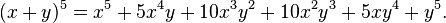


0 comments:
Post a Comment