Sunday, May 31, 2009
BOOOOOBBBB!!!!!!
Well this unit has practically zoomed by and, for me, has been the easiest unit of them all. It was made especially easy by the fact that there were only a very small number of formulas to memorize and a lot of graphs and patterns. The only thing I really need to remember for these is how to find the focuses on ellipses and how to graph a hyperbola.
Ellipses
take the square root of the difference between the semi-major axis squared and the semi-minor axis squared. this is how far, along the major axis, the foci's are from the center.
Hyperbola
first you need to draw the box created by the conjugate and semi transverse axises. from there you can draw the diagonal lines that make up the asymptotes of the hyperbola. Each one intersects the two opposite points on this box that has been created. Now take the lengths of the conjugate axis and the semi-transverse axis. Now square both of them and add them together. Then take the square root of that to find the distance between the centre and one of the foci's.
Well that is practically everything that I can think of at the moment so Wish Me Luck!!
See you guys in class.
Jessi
Long Distance BOB....Will You Accept The Conic Charges?
Man this unit just zoomed by! It's making me realize that in a couple weeks, I, along with the rest of us grade 12 math takers, will be taking the provincial exam for math. (I'm kinda nervous but I think I'll pull it off. :D)
I'll have to admit that at first, Conics sounded really intimidating. For me, it was because we had to deal with graphing parabolas/circles/hyperbolas/ellipses and see the patterns that accompany them and I really dislike parabolas and graphing them. I'm more of a problem solver and equation person. I guess as the unit went on, a lot of the stuff came pretty easy to me and the unit became easier. I learned to recognize the patterns easily and pull off a "Matrix"-esque move in math. We all learned how to do that didn't we? I think that's pretty awesome.
The easiest part of this unit was learning the different patterns and remembering what stood for what in each equation. I may not remember a lot of things, but for some reason, I do remember things relating to math fairly well. I also felt that how and why the equations worked was pretty interesting. 8)
The hardest part of this unit was the word problems. It's only because I end up thinking about the wrong things, but then again that might just be a coincidence. Hopefully, with the practice I took today with those types of problems, I'll be able to conquer them with ease. Graphing wasn't as hard as I thought it would be, but it was a pain (but that's just me being lazy xD).
I feel that there's only a couple things I need to remember for this test. One of these things being the pictures relating to the parabola/circle/ellipse/hyperbola showing how each parameter relates to the other. The second of these things being the equations for each of the conic chapes.
Parabola:
(x-h)2=4p(y-k) [vertical]
(y-k)2=4p(x-h) [horizontal]
(h,k)=Vertex
p=distance from vertex to directrix or vertex to focus point
Circle:
(x-h)2+(y-k)2=r2
r=radius
(h,k)=center
Ellipse:
[(x-h)2/a2]+[(y-k)2/b2]=1 {horizontal}
[(y-k)2/a2]+[(x-h)2/b2]=1 {vertical}
a=semimajor axis
b=semiminor axis
(h,k)=center
Hyperbola:
[(x-h)2/a2]-[(y-k)2/b2]=1 {horizontal}
[(y-k)2/a2]-[(x-h)2/b2]=1 {vertical}
a= transverse axis
b= conjugate axis
(h,k)=center
If I remember all this stuff, I think I'll do fine. I really am not too worried about this test.
Well, I guess that's all? I will see you all tomorrow! If you ahven't seen the intro to our (Dion, Mary, me) DEV yet, you can view it by clicking the link in the previous post (which should be very short :D). Hopefully, our DEV will be able to fulfill your expectations after watching the intro.
pc
~jayp~
Thursday, May 28, 2009
BOB on Conics
On with my BOB!
Honestly, this unit sounded intimidating, but in the end, it really wasn't at all! After I got past getting the hang of the geometry, I actually started to enjoy it... (Except for sketching graphs, I always did despise doing that.) :]
So now that I pretty much get the jist of all the geometry involving parabolas, ellipses and hyperbolas, I think I'll do well in that aspect.
However...
Applying them to "realistic" situations won't be my cup of coffee (gonna have to load up on this tmrw huhu). I'm sure with a little more practice I'll have a full understanding of taking pieces of information and constructing the proper equation for it, but waugh! In due time...
What I found interesting was that when you take a line and "spin" it, you end up with two cones, and from there you can derive the parabola, ellipse, and hyperbola! I'd describe/post images of this, but Jessi's scribe post on Conics had very good ones already :].
Now, onto the guidelines which I shamefully hardly ever follow...
- Get at least some sleep! Actually, sleep immediately after you study, you'll remember your stuff better!
- Eat breakfast, brain food = awesome because you don't want to hear your stomach during the test and neither do we lol.
- Take your time, don't rush!
- Keep in mind the equations for vertical/horizontal parabolas, ellipses, and hyperbolas!
- Look at these equations and see the geometry! Remember, "codes!"
- a^2 + b^2 = c^2!
- Be able to take very little given information and build upon them to end up with an equation that will help you out big time!
To everyone who's going on that Kenora trip tmrw... Bye. >_> Just kidding, have fun!
To everyone else, good luck on the test tmrw! :D
BOB for Conics
The most interesting thing I learned and most useful was the anatomy of the Hyperbola.
 This mini box allows us to find the hyperbola with ease and with less information required. Like if you have the conjugate axis and transverse you can find everything else like the asymptotes, vertex and center. Or if you have the slope of the asymptote and know the coordinates of an axis then you can find all the rest of the information also. Hyperbolas involve the difference of distances will always be constant.
This mini box allows us to find the hyperbola with ease and with less information required. Like if you have the conjugate axis and transverse you can find everything else like the asymptotes, vertex and center. Or if you have the slope of the asymptote and know the coordinates of an axis then you can find all the rest of the information also. Hyperbolas involve the difference of distances will always be constant.((x-h)^2)/(a^2) - ((y-k)^2)/(b^2)
+ or - determines whether its vertical or horizontal. Positive x = horizontal, negative x = vertical.
The ellipse was quite interesting. I was quite amazed that it does not have a radius but instead foci that help determine the value of c. Also within it are the major axis and minor axis. Which help determine the value of a and b in the standard form equation:
((x-h)^2)/(a^2) + ((y-k)^2)/(b^2)
the a and b's are switched in a vertical ellipse.
All in all it was short, but very straight forward. Mr.K said we should see the geometry when we see the equations like in the matrix where it shows code but they see people. I can safely say I'm ready and hope they're no big surprises.
Bobing for conics
k for this up coming test i made sure to keep an eye out on the hyperbola because i thought that it might be the hardest in the conics unit.
-hyperbola is identified by having both x^2 and y^2 and is the difference between the two
-opens vertically if y is positive and horizontally if x is positive
-finding the foci is found by add the square of the minor transverse axis and minor conjugate axis. Like a^2 + b^2 = c^2
The rest of the conics; circle, ellipse, and parabola I'm gonna go over some more.
Best of luck guys for tomorrow!
Oh one last thing i just remembered about conics, remember the pattern i think or the geometry of the object in order to give yourself a picture.
I believe that's what I'm trying to say...
ha ha well good luck again!
BOB
1. The general equation of a conic is
 .
.2. Completing the square is done to convert an equation's general form to standard form.
3. An ellipse has two axes of symmetry: the major axis and the minor axis.
4. If a hyperbola is parallel to the x axis, then x^2 is positive. If it is parallel to the y axis, then y^2 is positive.
5. (h,k) is the center of the conic.
6.a is the transverse axis in a hyperbola, while b is the conjugate axis. they indicate whether the hyperbola will be opening up and down, or left and right.
7. A parabola has only one variable squared, unlike the other ones.
Okay, good luck to everyone on the test! I know we'll all do well on it. :)
Night!
BOB not just sweet words
Success for the test(?):
- remember the formulas/equations!
- when we see the equations were suppose to see the graph!
- completing the square
- practice makes close to perfect
- eat, sleep and study
- confidence!
Good luck on the test tomorrow, study, study study.
-jennifer
bob
I was on this net to review
http://webct.merlin.mb.ca/webct/urw/lc4130001.tp0/cobaltMainFrame.dowebct
i didn't find the foci, and how you solve that part.
I still didn't get the foci, and i think I'm good with other stuff.
good luck guys!!!!!
BOB
I actually found this one interesting, since it felt cool when I successfully completed a question that asked me to graph something. Makes me feel like some kind of pro artist. :P Anyways, I struggled a little in the beginning. -Not- because it was hard, but because of some other issues that were affecting my work ethic.
I'm fairly confident about this test. I'm hoping to to get atleast 50% on it (just the passing. :P) but if I do better, then boo yeah. And yeah, I know I should "aim higher", but I'm just being realistic.
I won't bother going over anything, since everyone else probably will be doing it. (And better, I might add.)
Good luck on the test tomorrow.
-ConstantEcho
BOB on Conics
So, this unit was mainly about circles, parabolas, ellipses and hyperbolas...
For each of the stated above, we learned that each of them comes from a line that is spinned in a circle, basically, forming two cones. Depending on how you slice it, you can get one of the shapes/graphs/etc, stated above. We also learned the equations for each of the stated above. After Mr. K's talk about the matrix and such, he said we should also be able to identify what it is and what it looks like just by looking at the "code" or equation. I tagged a delicious link that can help you with this a bit, so if you're interested here it is!
Basically:
Parabolas - only have one squared term (ex. x^2 + y = 1)
Circles - have 2 squared terms that have equal coefficients (ex. x^2 +y^2 = 1)
Ellipses - hav 2 squared terms whose coefficients are not equal (ex. 2x^2 +y^2 = 1)
Hyperbolas - (I'm not 100 percent sure because i wasn't here for class that day, but from what I've seen...) have two squared terms, one being positive and one being negative? (ex. x^2 - y^2 = 0).
Another thing we learned was to change equations to general form from standard form and vice-versa.
I'm pretty sure i covered most of what we learned. I know there's more stuff, like the pythagorean theorum and such being used in the ellipse and hyperbola graphs, but I don't think I currently have enough skills to explain it.
What i found hard (until today) was finding the asymptote lines of the hyperbolas, but Mr. K. cleared that up for me.
Well, that's all I'm going to put up for my BOB.
Good Luck on the test everyone!
Jonno- Out
BOB

there is a little diagram of how the shapes were formed.
Circle formula:

Elipse formula:
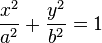
Parabola formula:
 or horizontal parabola:
or horizontal parabola:
Hyperbola formula:

I hope everyone gets an A+! don't forget about DEV projects
Conics BOB~
What we learned:
Parabolas
- vertex (h,k), a directrix (straight line, fixed distance from vertex), and focus(fixed distance from vertex)
- Standard form VERTICAL:

- Standard form HORIZONTAL:

- When 4p, also known as a, is greater than 1 the parabola is wide.
- When 4p is less than 1 the parabola is skinny.
Ellipses
- center (h,k), Vertices's (endpoints on Major axis), major axis (length of 2a), semi-major axis (length of a, center to one of the vertices's), Minor axis (legnth of 2b), Semi-minor (length b),Foci (c units from center), Focal radi (distance b/w Foci and point on ellipses.
- The midpoint of two foci would center of ellipses.
- Standard form HORIZONTAL:

- Standard form VERTICAL:

- a^2 is the bigger number.
- c^2 = a^2 - b^2
- center (h,k), Transverse axis (the distance b/w the vertices's, which are also the vertex. Is the difference of foci to pt, foci2 to pt. length of 2a), semi-transverse axis ( a),conjugate axis (length of 2b), Sem-iconjigate (b), Foci (c units from center), asymptotes.
- Standard form HORIZONTAL:

- Standard form VERTICAL:

- c^2 = a^2 + b^2
- When given slope of asymptotes, you can figure out the value of b or a. b/a = rise over run.
study hard guys!
BOB likes to eat icecream [cones]
I think that for this unit I just need to make sure I know the formulas really REALLY well. Let's review shall we ^__^
A PARABOLA:
The equations:

If the x is squared, the parabola is vertical (either opens up or down) and if the y is squared the parabola opens horizontally (opens left or right). p is the distance from the vertex to the directrix and the focal point. If 4p is a big number, the stretch of the parabola is also big. If the number is smaller than one the parabola will be skinny.
A CIRCLE:
The equation:

r is the radius. In general form, the coefficients of x and y are squared and are the same. That's how you know it's a circle!
AN ELLIPSE:
The equations:

When a (the bigger number) is under x, the ellipse is horizontal. If it's under y then its vertical.
a is the length of the semi major axis. b is the length of the minor axis. Use c^2 = a^2 - b^2 if you have to find the distance between the origin and the focal points. In general form, the coefficients for x and y are different.
A(N) HYPERBOLA:
The equations:

When x is positive the hyperbola is horizontal (opens right and left). When y is positive it is vertical (up and down). a is the length of the semi transverse axis, while b is the length of the semi conjugate axis.
use c^2 = a^2 + b^2 to find c, the distance from the origin to the focal points.
hyperbola graphs have asymptotes! use the slope formula to figure out their equations.
To be alright for the test, all we need to know are the formulas and how to graph them. I'm sure everyone will do fine! ;D
Make sure to eat healthy, drink plenty of water and get some rest so you can be in top shape tomorrow morning!
~Bye bye! :D
Wednesday, May 27, 2009
BOB for Conics
Anyhow, i just do this BOB briefly.
I think this unit is not really, you just need to know the formula and understand the graph so you could know which formula is parabola, ellipse, or hyperbola.
About the formula, i think some of us already posted it, so i am not going to repeat it. :D
Anyway, Good luck all guys, test on Friday and don't forget your delicious link [which i also almost forgot :-"] ...
13013 = BOB
Well this unit... Even though it took us like a week to study this unit, I don't think it was that short. Because the content's short, or that I actually absorbed all the necessary information in that amount of time; I do not know.
Well the hard part in this unit was the golf dome ellipse question. I don't know how to get the answer. It's quite complicated for me. Everything except that is all cool.
For tomorrow:
Remember the formulas!
Remember the rules like the axes, how to get the foci points, etc.!
Remember how each of the four things looks like in a graph!
Fellow classmates, give everything what you've got tomorrow!
BOB BOB BOB BOB :)
This unit went by really fast, and since it's the end of the school year, I'm becoming more lazy, so that means that I really haven't been paying much attention to a lot of things happening in class. So I really need to study a lot and make sure I do well on this test! The only thing I really need to review is the day when we learned about graphing parabolic equations since I wasn't in class for that lesson. I have a feeling it's not a hard thing to pick up, so hopefully I learn everything I need to know before our test, which is on friday. Other than that, I think I'll be okay. I'll just have to read through the slides to refresh my memory, and hope that I do well. I guess that's all, good luck! :)
BOBS on Conics?
So the first thing we learnt about was parabolas. We learnt another formula for a parabola which is :

P is the distance from your foci to your vertex or your distance from your directrix to your vertex.
If you want the horzontal graph, you just switch the (x-h) and (y-k).
The next thing we learned was circles and the formula is the same as the one we learned before so I'm not going to go into detail with that.
Then comes the elipses with the formula:

Where "a" is the length of the semi major axis and "b" is the semi minor axis.
If you want the vertical graph you just exchange the "a" and "b"
Then there's hyperbolas (parabolas on steriods, according to Mr. K)

Where "a" is your semi transverse axis and "b" is your semi congurant axis. If you want your vertical graph you just make "x" negative instead of "y".
So that's basically the simple summary of what we learn, time for my nap. Night.
Reflection on Conics
Good luck to everyone!
Is it a parabola? is it an ellipse? no its.. BOB
What are the chances this is a scribe post?


BOB
I know we have to know about ellipses and hyperbolas and that we need to know how to graph them, but I feel that there are going to be a lot of problems on the test that will require us to use our indepth knoweledge of these ellipses and hyperbolas, that I just won't know. I'm expecting a test that will be very tricky for me, with lots of curve balls coming from no where.
I hope that I and my fellow class mates can get enough studying in to do WonderfullyExcelent on this test, and I hope everyone has more knowledge than me on this unit going into this test.
Best of Luck! Alex.
BOB for Conics
Now its time to do the OTHER math homework that I have been procrastinating on...
Well this is my Bob for the conics unit. I found this unit pretty easy, except for the moments where I was just confused... or couldn't remember the equation for a circle... I think the test will be pretty easy as long as I don't do anything stupid like get an ellipse and a hyperbola mixed up.
Hmmm well what is important for this unit?
1. Equations for...
parabola: (x-h)^2 = 4p(y-k) (vertical) and (y-k)^2= 4p (x-h) (horizontal)
Circle: (x-h)^2 + (y-k)^2= r^2 (standard form)
Ellipse: (x-h)^2 / a^2 + (y-k)^2 / b^2 = 1 (horizontal) and (x-h)^2 / b^2 + (y-k)^2 / a^2 = 1 (vertical)
Hyperbola: (x-h)^2 / a^2 - (y-k)^2 / b^2 = 1 (horizontal) and (y-k)^2 / a^2 - (x-h)^2 / b^2 = 1 (vertical)
So for the test i think we just need to make sure to know all the parts of shapes and how everything fits together. Remember how to find the vertices, foci, center, radius and length of major and minor axis! I think that's all I have to say for this unit. Just remember to get lots of sleep, (something I need), DON'T eat a ton of candy and study the formulas! :D


Scribe and Bob Post
Quite a number of people have asked to see my Counting test, so I just scanned it and decided to post it here. Page 1 Page 2 Page 3 Page 4 I found this unit extremely easy. The stuff looked like nonsense and garbage to me from the start, but when I actually looked at the stuff, I realized that I was wrong. The folding of the papers did not help me however. Nevertheless, it was Mr. K’s method to help us understand every one of the conic sections. You must basically understand the anatomy of each conic section. That is the key to solving the questions. Other than that, the unit test should be easy. Well, I hope it is. WATCH OUT WHEN DOING/DRAWING THE VERTICES AND FOCII. IT’S OBVIOUS THEY’RE NOT THE SAME, BUT EVEN PEOPLE THAT KNOW THAT CAN MAKE MISTAKES WHEN DRAWING THEM. SOME PEOPLE USE THE FOCII AS THE VERTEX BY ACCIDENT OR ADDRESS THEM INCORRECTLY WHEN ANSWERING QUESTIONS !!!!! Hyperbola The transverse axis extends from the vertices of the hyperbola. This does not have a fixed orientation. It can be either horizontal or vertical. It can be found by using “2a.” Two semi-transverse axes complete a full transverse axis. The conjugate axis is the perpendicular bisector of the transverse axis, meaning it cuts the transverse axis in half at a 90 degree angle. This does not have a fixed orientation. It can be either horizontal or vertical. It can be found by using “2b.”Two semi-conjugate axes complete a full conjugate axis. For the conjugate and transverse axes, watch out for what the question asks for. Some may ask for the “semi axis” while some may ask for just the “axis.”
Ellipse Worksheet on Ellipse The major axis is the longest of the axes. Two semi-major axes complete the major axis. The minor axis is the shortest of the axes. Two semi-minor axes complete the minor axis.
Circle Video on Circle Worksheet on Circles The circle is like the ellipse’s brother. They’re pretty much the same except the circle has radii equidistant from the circumference to the center of the circle. Parabola Video on Parabola Worksheet on Parabola The parabola is very easy to understand. There is one focus which is the same distance as the directrix from the vertex of the parabola. Question If the focus is to the left of the vertex, what direction does the parabola open? It opens to the left.  Probability |









