----------------------------------------------------------------------------------
The natural way of measuring angles in a circle is using Radians. A Radian is the radius of a circle along its circumference.
----------------------------------------------------------------------------------
This is where Pi comes into play. Pi is 3.1415926535.....so on. Which is the amount of radians in 180 degrees of a circle. This example below is a great picture of what a radian is. It is just an equilateral triangle pressed down. It now looks more like it fits in a circle, and as you can tell the degrees is now lower than 60. Which gives us that .1415926535... difference. So 180 degrees is equivalent to Pi in radians.

----------------------------------------------------------------------------------
The formula to convert from degrees to radians and vice versa is below for those who need to see it this way. "R" represents the angle in radians, "D" represents the angle in degrees. The symbol BELOW the "R" is known as Pi. This is just the relationship between Radians and Degrees.
 ----------------------------------------------------------------------------------
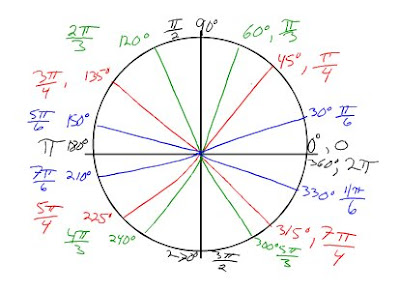
----------------------------------------------------------------------------------Below is a picture of simple degree values and there Radians beside it. To better understand this picture as it may be hard to look at, I will provide a couple examples. Remember that Pi is equal to 180 degrees.
Example 1: 30 degrees in a circle is Pi/6. That is because 30 degrees is only 1/6 of 180. So if you think about this with Pi, it also contains that same relationship. So a sixth of Pi is Pi/6.
Example 2: You have 225 degrees, which is 5Pi/4 on the circle. 225 degrees is 45 more than 180. Which also means its Pi/4 more if you understand that 45/180 is 1/4. So since it is between Pi and 2 Pi. Add Pi to Pi/4 and you will get 5Pi/4 that is given on the circle. Pi can be added since you have already completed that part of the circle.
 ----------------------------------------------------------------------------------
----------------------------------------------------------------------------------
Well that's about it. I'm sorry for this late post, and if my information was not at all helpful I'm sorry and will try to make it better for my next post. All these diagrams were slides from our classroom. Also don't forget about the homework that was assigned (Exercise 1: 1-10, Exercise 2: 1-10, and choose 5 from 11-20.) The next person I choose to scribe is Ingrid!


Nice post Anthony!!! Nice use of colours, It made it easy to pick out the important information. Good job!
ReplyDeleteI especially like the picture you provided of the "squished" equilateral triangle. I almost stole it... And might still some day. It made me wonder which has a greater area -- the equilateral triangle or the 1 radian wedge? My gut tells me the wedge.
ReplyDelete