February 5th: Learning Within Groups

Good evening fellow classmates, Ingrid here to scribe for today's classroom events!

We started off the class by being introduced to a less than common approach to learning when it comes to math; group learning!
We were assigned numbers and assembled into groups according to those numbers. As a group, we situated ourselves in a section of the room in order to work as a team for the remainder of the class.

First off, we worked on a question similar to a previous question we were given where we looked for the degree amount a wheel traveled, only this time, we looked for it in radians.


Alright, keeping in mind the proportion of the sector we are looking for to the proportion of an entire circle, we can see that by using the values given, we can easily solve for the variable; in this case theta (θ), which is in radians.

After solving this problem we then discussed how:

The radian is simply the radius of a circle wrapped around the circumference of the circle.

Therefore;
half a circle is approximately 3 radians (π) and
a full circle is approximately 6 radians (2π).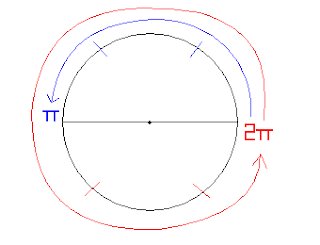(Please pardon my poor excuse of a diagram lol.)

We then worked on a new problem where we were to find the number of radians between the minute and hour hands of a clock at 4:00. This produced one question courtesy of yours truly, which PJ bravely asked Mr. Kuropatwa, that is: "Which arc to we look for?" In the end, we solved for both :]

Here is the solution I particularly liked for its simplicity (the one on the right hand side of the vertical line), courtesy of Mary... Or was it PJ? XD;

Since we know that 2π = 360° (a full circle), and that there are 12 sectors on a clock, we can divide 2π or 360° by 12 to find the number of radians or the degree amount of each sector.
We then find it to be π/6 (radians) or 30° per sector.
From here we can easily figure out the number of radians or the degree amount between the hour and minute hand (the smaller arc). Since we know there are 4 sectors between them, we can multiply the values we found for one sector by four.
We find them to be 2π/3 or 120°.
To find the number of radians or degree amount between the hour and minute hand with regards to the larger arc, we simply subtract those values from our full circle values. That is:

or

Mind you, this was only one way of solving this problem. Other students offered other methods and they can be easily viewed in the slideshow from today. :]

Afterwards, Mr. K made a reference to the Ancient Sumerians and how they derived 360° from the calendar and used that method to find the degree amount in one sector of a clock. That is, there are 12 months in a year, and 30 days in a month. Similarly, there are 12 hours in a day, and 30 days in a month... Multiply those two numbers together and you have 360! It is then easy to see that there are 30° in one sector of a clock.

PHEW! This is getting lengthy but I swear, I'm almost done!

We elaborated a bit on a new term: coterminal.
First off, we defined an angle to be in standard position when the intial side lies on the positive x-axis.
Therefore, coterminal angles mean two angles that start at standard position, but travel in opposite directions, however, still ending at the same place - together.

Finally, we were given one more question where we were to find the area of a sector of a circle. Again, by using the idea of proportionality, this can be easily solved.

All in all the point of today's class was to realize that there are many many many ways to solve a problem. But we must always keep in mind the relationship between the proportions!

Tonight's homework is the 5 questions you did not choose to answer from last night's assignment (Exercise 2: #11-20).

And in return for whipping a dodgeball at my face; Aldrin will be the next scribe :D!