Anywayyyyys... today we started off class with Mr. K very likely confusing or scaring our parents by implementing use of the "yackpack" tool on the blog. he first announced who we were ( We come in peace?) and then we all just sorta started to laugh, and now some of our parents are wondering why they are suddenly the stars of a latest sitcom ( My Child the Precal Student, perhaps?)
Ah, but I digress, back to the math! After our excitement died down a bit, the slideshow appeared, in all it's magical Smart Board glory. A very similar premiere slide appeared today, now with a new caption. Today we were to delve into the wonder that is solving trigonometric equations! (really this time).
We started out with some fairly simple questions reminiscent of the day before. Determine trigonometric values and come to an exact value as an answer. Here are the questions along with some straight-forward solutions.

Something Mr. K touched upon was the concept that we don't exactly NEED to rationalize the denominator anymore as far as radicals go. No matter where you put the radical, it's still there. and sometimes it's probably even more handy to eliminate radicals from the numerator and have them all on the denominator, but I used the answer where we do rationalize radicals in the denominator. Heavy stuff...
Yesterday we had also started to talk about phi, or  if the symbol interests you at all. Phi as a refresher, is just another fun Greek letter/symbol (huzzah for the Greeks!) meaning the related angle of "theta". Today we started investigating the use of it a little bit more.
if the symbol interests you at all. Phi as a refresher, is just another fun Greek letter/symbol (huzzah for the Greeks!) meaning the related angle of "theta". Today we started investigating the use of it a little bit more.
Now we started doing questions using the inverse, or arc, trigonometric functions. For each given value, we should end up with 2 different angles (except of course, in the case of 90,180.270, and 360 degrees.) To spice things up a little bit - solving for the angles in radians. I won't bother with the first question of the type because it's basically a question we all know and love using a common sin value on the unit circle. For those who need it, the answers result in Pi/4 or 3Pi/4.
It was after this question that "Phi" came in.
Here are the 2 questions we solved using phi: 

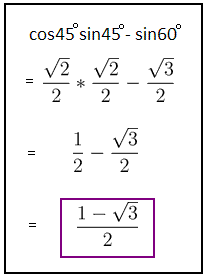



0 comments:
Post a Comment