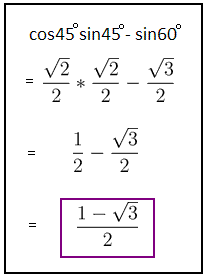EDIT~
3.14159..
hey guys! It's mary here and as your scribe from yesterday, i'll be summarizing the wonderful moments of precal class...today. Sorry about leaving you with that cliff hanger last night. But as promised, i will finish the post.
For yesterday’s class, we learned..
~ What the sine and cos graphs looks like and why the way it does.
~ The
difference between the sine and cos graph, along
with the meaning of
amplitude and
period.
~ What a sinusoidal axis is.
~ The 4 ways you can alter a sine or cos graph. (Translations)
1a) Sine Graph: .JPG) wow, the image quality sucks. LOL bare with me!
wow, the image quality sucks. LOL bare with me!
Okay, so in order to explain the graph, you must understand the unit circle. As you go around the unit circle, starting from zero(or 2/pi), the sin value
increases than decreases. The Sine
value goes from 0, 1, 0, -1, and back to 0 again as it makes it full circle. It has a
max value of 1 (when reaches /pi/2, and a min value of -1 (when reaches 3/pi/2).

Regarding the unit circle, the
sine graph displays the sine values as you travel around the unit circle, in a way where we can see that pattern. (of 0, 1, 0, -1, 0). This means the
y-axis on the graph
shows the sin value, while the
x-axis shows the distance traveled on the unit circle. (2/pi, /pi/2, /pi, 3/pi/2 etc).
Understanding this would come in handy when asked to draw a sine graph. 10 points for those who can understand the relationship!
(brownie points) if not, ask yourself this: "where does sin equal zero on the unit circle?" look at the sine graph, "where does sin equal 1 and -1 on the unit circle?" then look at the graph. Your answers should be the same as the answers on the graph. "zero,2/pi, /pi, /pi/2 and 3/pi/2". 1b) Cosine Graph.bmp)
Again, just like with the Sine Graph, the y-axis on the graph shows the cos value, while the x-axis shows the distance traveled on the unit circle.
2a) Sine Graph vs. Cosine Graph
The Sine Graphs and the Cosine Graphs are pretty much the same. The only difference is, cos is horizontally shifted, /pi/2 units to the left, on the x-axis, from the sine graph . This means, if you were to take a Sine Graph, and push it /pi/2 units to the left, you would have a Cos graph. And if you were to take a Cos Graph and pull it /pi/2 units to the right, you would have a Sine graph. "They are identical in amplitude, period, domain and range". I hope you guys can understand the picture below. I was trying to show you visually that the two graphs are /pi/2 units away from each other.

2b) UH OH, new terms?! don't worry, i got this! ;)
--------------------------------------
mary says:
whats Period and Amplitude again? -__-
pj says:
Period is how long it takes for 1 cycle to repeat
pj says:
Amplitude is the distance from the highest points to the average
mary says:
so 2pi?
pj says:
it's 2pi for the regular sine/cosine curve
-----------------------------------------
Sinusoidal Axis: "Sinusoidal axis: is the line which passes directly through the center of the sin curve horizontally. This line is always parallel to the X axis if it is not the X axis to begin with." The sinusoidal axis is used as a reference line when altering your sin or cos graph. Remember, its not actully part of the graph, so don't draw it on a test, unless told to.

ALMOST DONE, STAY WITH ME GUYS!
3a) Translation:
When graphing trig functions, there are four ways it can be altered. (from its regular form, sin(x) or cos(x).)
Shifting it up/down. (vertical shift)
Shifting it left/right. (horizontal shift)
Stretching it vertically.
Compressing it vertically.
~Vertical shift (Shifting it up/down) this would go the same for cos and sine
example: (because its more effective than me blabbing away) sin(x)-2
the negative 2 would move the max and min values, of the graph, two units down. Another way of looking at it, would be having the new sinusoidal axis two units down from the previous. In this case, the sinusoidal axis would go from 0 (x-axis) to -2. Then you would just draw the graph as you would from the new sinusoidal axis.
example: sin(x)
+2Just like before, but the positive 2 would move the max and min values, of the graph, two units up.
~Horizontal shift(Shifting it left/right) this would go the same for cos and sine
example: sin(x-2)
the negative 2 would move the of the graph, two units right, from the regular sin graph. Notice how i said right, not left.

example: sin(x+2)
the positive 2 would move the of the graph, two units left, from the regular sin graph.

~Stretching&Compressing it
example: sin(2x). sin(1/2x)
The 2 would compress the graph, twice as much. While the fraction, 1/2, would stretch it twice as much.

3b) Translation order; DABC!
Most of the time, you will be faced with a combination of these translations. (vertical/horizontal shift, compress/stretch). And there is a order you go by, when you have to draw them. D A B C
From AsinB(x+C)+D or AsinB(x-C)+D, you would use DABC. Meaning you would do the vertical shifts first, since D is first in order.
Okay, enough of the snore-fest!
IMPORTANT NOTICES!
1) Mr. K will not be in class for the rest of this week, and the following week after. Reason: because of a family emergency. But
show no fear,(that one was for you
pj!), Mr. k had said he’ll keep in touch with us through the blog, and
I'm sure everything will work out with Mr. K's situation.
2) Also, there is still an
unit test on Friday,
FEBRUARY 20
th. Study hard and good luck :D
Resources:
http://www.cbv.ns.ca/mathhelp/P66.htmhttp://www.clarku.edu/~djoyce/trig/http://www.fooplot.com/
Next scribe will be laika~












.bmp) Again, just like with the Sine Graph, the y-axis on the graph shows the cos value, while the x-axis shows the distance traveled on the unit circle.
Again, just like with the Sine Graph, the y-axis on the graph shows the cos value, while the x-axis shows the distance traveled on the unit circle.
 Why would I point this out? Because I had such a wonderful time writing out the (wrong xD) answers on the slide it was from. No, actually Mr. K pointed out that on our exam we have to write the answers that don't work or that are undefined seperate from the answers that DO work. Also, for those of you wondering why cos x = 2 is undefined, it's because the unit circle has a radius of one and the maximum unit that it can go up to is one. Two unfortunetly is too big. D=
Why would I point this out? Because I had such a wonderful time writing out the (wrong xD) answers on the slide it was from. No, actually Mr. K pointed out that on our exam we have to write the answers that don't work or that are undefined seperate from the answers that DO work. Also, for those of you wondering why cos x = 2 is undefined, it's because the unit circle has a radius of one and the maximum unit that it can go up to is one. Two unfortunetly is too big. D=